\(\newcommand\F[2]{\mathit{#1}\left(#2\right)}\) \(\newcommand{\minR}{\mathit{min_r}}\) \(\newcommand{\maxR}{\mathit{max_r}}\) \(\newcommand{\tmult}{\cdot}\) \(\newcommand\static[1]{\F{static}{#1}}\) \(\newcommand{\sfr}{\frac{1}{1600}}\) \(\newcommand\tc{\tau_c}\) \(\newcommand\tr{\tau_r}\) \(\newcommand\grf{\gamma}\) \(\newcommand\dyn[1]{\F{dyn}{#1}}\) \(\newcommand\sgn[1]{\F{sign}{#1}}\) \(\newcommand\dist[1]{\F{distance}{#1}}\) \(\newcommand\DTF{{\Delta t}}\) \(\newcommand\IL[1]{\normalsize{#1}}\) \(\newcommand\MX[2]{\F{max}{#1,#2}}\) \(\newcommand\adr[1]{\F{adaptive}{#1}}\) \(\newcommand\clip[3]{\F{clip}{#1,#2,#3}}\) \(\newcommand\supply[1]{\F{supply}{#1}}\) \(\newcommand\iss[1]{\F{issuance}{#1}}\) \(\newcommand\isb[1]{\F{issuance_{block}}{#1}}\) \(\newcommand\tw{\Sigma_w}\) \(\newcommand\rw[2]{\F{reward_{#1}}{#2}}\) \(\newcommand\tip[2]{\F{tip_{#1}}{#2}}\) \(\newcommand\lbs[1]{\F{subsidy_{LB}}{#1}}\) \(\newcommand\exp[1]{\F{exp}{#1}}\) \(\newcommand{\vdf}{\mathit{VDF}}\)

TL;DR This document provides a high-level functional specification for Adaptive Issuance and Staking, two new features of the Oxford protocol upgrade proposal, which together constitute a major evolution of Tezos’ Proof-of-Stake mechanism.

• NB 27/03/2024 The features described in this documment have not been included in the Oxford 2 protocol, currently active on Tezos Mainnet. See Oxford 2’s announcement for further detail. The Paris protocol proposals implement revisited version of these features.

• EDITED on 02/10/2023 to correct the value for \(\IL{\grf}\)¹ in the dynamic rate formula, which did not reflect the value used in its implementation in Oxford.

Adaptive Issuance

Adaptive Issuance is a novel mechanism regulating tez issuance in Tezos.

Currently, the Tezos economic protocol issues new tez via:

• Participation rewards: incentives given to delegates for participation in consensus and random seed generation.
• The Liquidity Baking (LB) subsidy.
• Protocol “invoices”: lump sums of tez issued and allocated during protocol migration.

Participation rewards and the LB subsidy are regularly issued by the protocol, whereas the value and recipients of invoices are defined discretionarily by the developers of a protocol proposal. In the Nairobi protocol, and in previous ones, the values for participation rewards and the LB subsidy, if any, are defined by the Tezos protocol using fixed constants.

The Oxford protocol proposal introduces Adaptive Issuance: a mechanism where the amount of regularly issued tez (participation rewards and the LB subsidy, if active) depends on the global staked funds ratio — that is, the ratio of staked tez to the total supply. This lets issuance roughly match the actual security budget the chain requires, the amount needed to encourage participants to stake and produce blocks, but no more.

At the end of each blockchain cycle, the regular issuance is adjusted, to nudge the staked funds ratio towards a protocol-defined target (set at 50% in Oxford). Participation rewards and the LB subsidy are recomputed to match that budget. When the staked funds ratio decreases and diverges from the target, emission rates increase, incentivizing participants to stake funds to re-approach the target. Conversely, incentives decrease as the ratio increases beyond the target.

Adaptive issuance rate

The adaptive issuance rate determines, at the end of cycle \(\IL{c}\), the issuance for cycle \(\IL{c + 5}\). The adaptive issuance rate is the sum of a static rate and a dynamic rate. The final result is clipped to ensure nominal emissions remain within \(\IL{[\minR,\ \maxR]}\) (set to [0.05%, 5%] in Oxford) of the total supply.

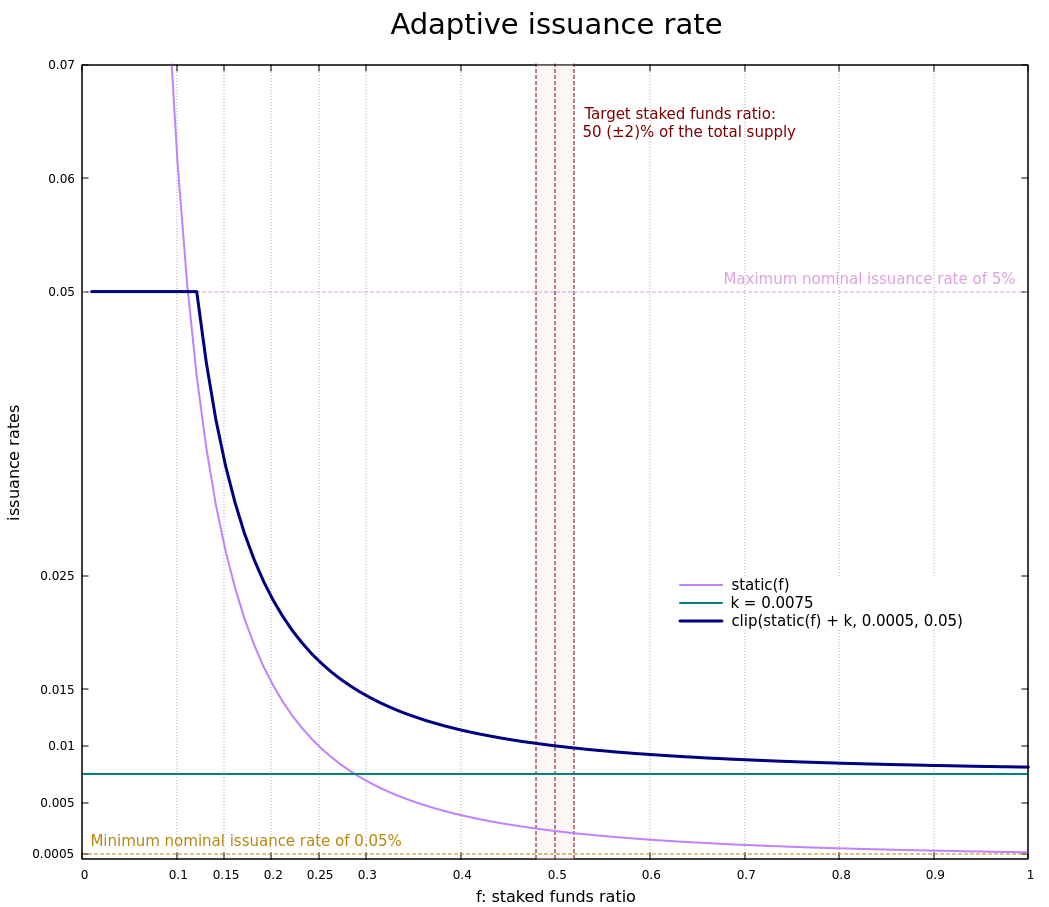
Figure 1 plots the nominal issuance rate and the static rate as a function of the staked ratio \(\IL{f}\). In the graph above, we picked the value 0.0075 (or 0.75%) for the dynamic rate, but this is just an example and that number varies dynamically over time.

The static rate is a static mechanism, which approximates a Dutch auction to compute a nominal issuance rate as a function of the staked funds ratio for a given cycle. Its value decreases as the staked funds ratio increases, and vice versa.

STATIC RATE    Let \(\IL{f}\) be the staked funds ratio at the end of cycle \(\IL{c}\). Then, the static rate is defined as:

\(\static{f} = \sfr \tmult \frac{1}{f^2}\)

The choice of \(\IL{\sfr}\) as a scaling factor ensures that the curve takes reasonable values for plausible staking ratios. Moreover, assuming Adaptive Issuance is activated with a dynamic ratio of 0, and at current staked funds ratio (that is, ~7.5% of the total supply), this factor allows for a smooth transition from current issuance rate (~4.6%).

The dynamic reward rate adjusts itself over time based on the distance between the staked funds ratio \(\IL{f}\) and the 50% (±2%) target ratio (\(\IL{\tc}\) and \(\IL{\tr}\) parameters below), increasing when \(\IL{f}\) < 48% and decreasing when \(\IL{f}\) > 52%, provided the total issuance rate is not hitting its lower or upper limit.

DYNAMIC RATE    The dynamic rate \(\IL{\dyn{c}}\) is defined at the end of cycle \(\IL{c}\) as:

\(\dyn{c} = \dyn{c -1} + \sgn{\tc - \F{f}{c}} \tmult \grf \tmult \dist{\F{f}{c}} \tmult {\Delta t}\)
\(\dyn{c_0} = 0\)

\(\IL{\dyn{c}}\) is then clipped to \(\IL{\left[ 0, \maxR - \static{\F{f}{c}}\right]}\), ensuring that \(\IL{\static{\F{f}{c}} + \dyn{c} \leq \maxR}\).

In this formula:

• \(\IL{c_0}\) is the first cycle where Adaptive Issuance is active.

• Given a cycle \(\IL{c}\), \(\IL{\F{f}{c}}\) denotes the staked funds ratio at the end of the cycle, and \(\IL{\dyn{c}}\) the value of the dynamic rate computed in that cycle.

• \(\IL{\tc}\) = 0.5 and \(\IL{\tr}\) = 0.02 denote, respectively, the target staked funds ratio and the radius of the interval centered on the target ratio.

• \(\IL{\grf}\) = 0.01, controls the speed at which the dynamic rate adjusts. The value is set so that a one percentage point deviation of the staked funds ratio changes the dynamic rate by 0.01 percentage points per day¹.

• \(\IL{\dist{\F{f}{c}} = \MX{0}{\left|\F{f}{c} - \tc \right| - \tr}}\) denotes the (absolute) distance between the staked funds ratio \(\IL{\F{f}{c}}\) and the interval \(\IL{\left[ \tc - \tr, \tc + \tr \right]}\).

• \(\IL{\DTF = \frac{16384 \tmult 15}{86400} = 2.8\overline{444}}\), denotes the minimal duration (in days) of a Tezos cycle, assuming all 16384 blocks in the cycle are produced at the minimal allowed time – that is, every 15 seconds.

• \(\IL{\sgn{\tc - \F{f}{c}} = 1}\) if \(\IL{\F{f}{c} \leq \tc}\) and \(-1\) otherwise, denotes the sign of the distance between the target ratio \(\IL{\tc}\) and the staked funds ratio \(\IL{\F{f}{c}}\).

In a nutshell, \(\IL{\dyn{c}}\) increases and decreases by an amount proportional to the distance between the target rate and the interval \(\IL{\left[ \tc - \tr, \tc + \tr \right]}\), while ensuring that the adaptive issuance rate is kept within \(\IL{[\minR,\ \maxR]}\) bounds.

Finally, as mentioned before, the nominal adaptive issuance rate² for a cycle \(\IL{c + 5}\) is defined as the sum of the static rate and the dynamic rate, clipped to stay within 0.05% — 5% range.

ADAPTIVE ISSUANCE RATE    Let \(\F{f}{c}\) be the staked funds ratio at the end of cycle \(\IL{c}\), the adaptive issuance rate for cycle \(\IL{c+5}\) is defined as:

\(\adr{c + 5} = \clip{\dyn{c} + \static{\F{f}{c}}}{\minR}{\maxR}\)

Adaptive rewards

In Nairobi, and in previous Tezos protocols, participation rewards and the LB subsidy are fixed values defined by protocol constants. With the proposed mechanism, the adaptive issuance rate provides instead a budget for the whole cycle, which gets allocated equally to each block of the cycle and distributed between the various rewards, in proportion to their relative weights.

ADAPTIVE ISSUANCE PER BLOCK    Let \(\supply{c}\) be the total supply at the end of cycle \(\IL{c}\), the issuance per block for cycle \(\IL{c+5}\) is defined as:

\(\isb{c + 5} = \frac{\adr{c + 5}}{2102400} \tmult \supply{c}\)

Where 2102400 = \(\IL{\frac{365 \tmult 24 \tmult 60 \tmult 60}{15}}\) is the maximal number of blocks produced in a year, given a minimal block time of 15 seconds.

REWARD WEIGHTS    The Oxford proposal defines the weights for participation rewards and the LB subsidy as:

• Attestation (formerly, endorsing) rewards : 10,240.
• Fixed baking reward: 5,120.
• Bonus baking reward: 5,120.
• LB subsidy: 1,280.
• Nonce revelation tip: 1.
• VDF tip: 1.

The total sum of all weights is \(\tw\) = 21762. The total issuance per block, \(\IL{\isb{c}}\), is distributed amongst the different rewards in proportion to their weight.

Consensus rewards. Since the adoption of Tenderbake, Tezos protocols have rewarded delegates for their participation in consensus with the following rewards per block:

• A fixed baking reward, given to the delegate which produced the payload of the block (i.e. choosing transactions, and other non-consensus operations).
• A variable, baking bonus reward given to the delegate which produced the block included in the chain. This bonus is given for including attestations, if their combined attesting power exceeds the minimal threshold (two thirds of total slots).
• A collective attestation reward shared between the delegates selected in the consensus committee for that block level, for attesting block proposals.

We refer to the technical documentation for further insight on the pre-requisites and distribution of these rewards. Here, we derive the new formulas which compute their values per block for a cycle \(\IL{c}\):

\(\rw{baking}{c} = \rw{bonus}{c} = \frac{5120}{\tw} \tmult \isb{c}\)
\(\rw{attestation}{c} = \frac{10240}{\tw} \tmult \isb{c}\)

Note that these formulas change the value of available rewards, but not why and how they are awarded. Hence, \(\IL{\rw{bonus}{c}}\) still denotes the maximal value for this reward: the actual reward issued depends on the total number of attested slots in a block. Similarly, \(\IL{\rw{attestation}{c}}\) is also a maximal value per block, which is further shared between multiple delegates depending on the number of attested slots and subject to the existing participation conditions.

Nonce and VDF revelation tips. The rewards allocated to delegates for contributing to random seed generation (that is for, revealing nonce seeds and posting VDF proofs) are not paid each block, but rather every 128 blocks. The adjusted formulas result:

\( \tip{\vdf}{c} = \tip{nr}{c} = 128 \tmult \frac{1}{\tw} \tmult \isb{c}\)

Liquidity baking subsidy. The LB subsidy per block is determined by the following formula:

\(\lbs{c} = \frac{1280}{\tw} \tmult \isb{c}\)

Note that while the subsidy is issued only if the feature is on, its weight is always counted in the computation of \(\IL{\tw}\). In other words, the budget for the LB subsidy is always allocated, regardless of whether it is issued or not.

The Oxford protocol proposal implements a new RPC endpoint, /issuance/expected_issuance, which reports the precomputed values of all participation rewards and the LB subsidy, for the cycle corresponding to the queried block level, and the next 4 cycles.

New Staking mechanism

Staking is an evolution of the existing Tezos Liquid Proof-of-Stake mechanism. It introduces a new role for network participants, called staker, complementary to the existing delegate (also known as baker) and delegator roles. A staker must also be a delegator — that is, they must first choose a delegate.

When stakers stake funds towards a delegate’s staking balance, the associated baking and voting powers accrue to that delegate. Similarly to how delegated funds work, staked funds remain within the staker’s account at all times.

Staked and delegated funds have different weights in the computation of delegates’ baking and voting powers: staked funds (both external stakes by stakers and the delegate’s own) count twice as much as delegated funds.

Unlike delegated funds, staked funds are considered to contribute to the security deposit associated with their chosen delegate. Thus, they are subject to slashing if the delegate misbehaves by double-signing block proposals or consensus operations, and are subject to the same withdrawal delays — colloquially, they are “frozen”.

Stakers are slashed proportionally to their contribution to the delegate’s staking balance. To simplify slashing, double-baking penalties are now proportional to staked funds: instead of the previous fixed sum of 640 tez they are now set to 10% of the delegate’s stake. Moreover, denunciation rewards (both for double-baking and double-attestations) are reduced from one half to one seventh of the slashed funds. The chosen value prevents adversarial delegates from abusing the slashing mechanism for profit at the expense of their stakers.

Delegates configure their staking policy by setting staking parameters which regulate whether they accept stakers (the default being to reject them), and if so, up to which fraction of their total staking balance. They can also configure which proportion of the staking rewards is set to accrue to their own staked balance versus their unfrozen, spendable balance. As participation rewards are paid to the staked balance, and automatically shared between delegates and their stakers, delegates can use this parameter to collect an edge from the rewards attributable to their stakers.

If and when Oxford activates, freezing and unfreezing of staked funds will be controlled directly by delegates and stakers, and will no longer be automatic. This entails that staked funds are frozen until manually unfrozen by stakers. This is a two step process which spans for at least 7 cycles (cf. Staked funds management).

A new user interface is provided for delegates and stakers to interact with the mechanism. It is based on four pseudo-operations: stake, unstake, finalize_unstake, and set_delegate_parameters. Pseudo-operations are self-transfers: a transfer operation where the destination matches the source – each involving a special entry-point of the same name introduced for implicit accounts. This approach was chosen to minimize the work required by wallets, custodians, exchanges, and other parties to support the functionality.

NB Until feature activation: only delegates can stake funds and the relative weight of staked and delegated funds remains unchanged. In the current implementation, only implicit accounts can become stakers. In other words, smart contracts cannot stake funds (they can of course still delegate them).

Staking policy configuration

Delegates can configure their staking policy by setting the following parameters:

• edge_of_baking_over_staking: a ratio between 0 and 1, whose default value is 1. This parameter determines the fraction of the rewards that accrue to the delegate’s liquid spendable balance — the remainder accrues to frozen stakes.
• limit_of_staking_over_baking: a non-negative number, denoting the maximum portion of external stake by stakers over the delegate’s own staked funds. It defaults to 0 — which entails that delegates do not accept external stakes by default. It is moreover capped by a global constant, set to 5 in Oxford, which ensures the baker controls a significant part of the stake.

Delegates can modify these staking parameters at all times, using the set_delegate_parameters pseudo-operation: that is, by transferring 0 tez to their own set_delegate_parameters. The chosen values for both parameters need to be supplied. The new parameters are then applied 5 cycles later.

On overstaking and overdelegation. Note that if a delegate’s limit_of_staking_over_baking is exceeded (that is, the delegate is overstaked), the exceeding stake is automatically considered a delegation for the delegate’s baking and voting power calculation, but it does remain slashable. The new mechanism does not alter overdelegation (delegated funds beyond 9 times the delegate’s own stake) nor its consequence on voting and baking powers. That is, overdelegated funds are not counted towards a delegate baking power, but they do increase their voting power.

Staked funds management

Stakers (and delegates) can use the stake, unstake, and finalize_unstake pseudo-operations to control their stakes. Figure 2 illustrates their effect on a staker’s funds. Note that while these pseudo-operations change the state of the involved funds, they remain otherwise within the staker’s account at all times.

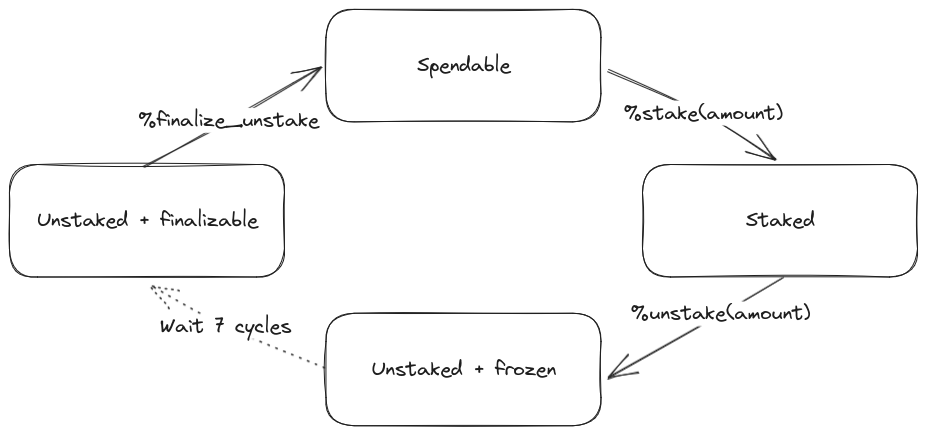
To stake funds, a delegator uses the stake pseudo-operation, transferring the chosen amount of spendable tez to their own stake entry-point. The staked tez will then be frozen and contribute to their chosen delegate’s staking balance. Note that the stake pseudo-operation will fail if the sender account is not delegated.

To unstake funds, a staker first submits an unstake request with the unstake pseudo-operation. This is implemented by transferring 0 tez to their unstake entrypoint, while passing the chosen amount as a parameter.

The requested amount will be unstaked but will remain frozen. After 7 cycles, unstaked frozen tokens are no longer considered at stake nor slashable. They are said then to be both unstaked and finalizable.

A staker can retrieve all unstaked and finalizable tokens at any time, making them spendable again. This is done using the finalize_unstake entrypoint — that is, by transferring 0 tez to their finalize_unstake entry-point.

Feature activation vs protocol activation

Should the Oxford protocol proposal be accepted by the community, and once the protocol becomes active on Tezos Mainnet, most of the features described in this document will not be enabled by default, only latent possibilities in the protocol, waiting for a separate activation.

In particular, the following changes will require additional approval from delegates via separate feature activation vote mechanism:

• Adaptive issuance — including notably the changes to the computation of consensus rewards and the LB subsidy.
• Ability for delegators to become stakers — until feature activation delegates continue to be the only participants who can stake funds.
• The changes in weight for staked and delegated funds towards the computation of baking and voting rights.

Other changes described earlier would be enabled from Oxford’s activation:

• The new interface for stake manipulation based on pseudo-operations. Note that this entails the deprecation of the set/unset deposits limit interface and also the end of automatic deposit freezing. On protocol activation, each delegate’s stake is derived from the frozen deposits at the end of the last cycle of Nairobi.
• The changes in slashing penalties (double-baking penalties are set to 10% of the staked funds) and denunciation rewards (they amount to one seventh of slashed funds).
• Changes to protocol constants. Note that this entails calculating participation rewards and the LB subsidy using the weight-based formulas, but these are defined so that they match the previous values when Adaptive Issuance is not active.

Activation Vote

We highlight the following principles behind the feature activation vote mechanism:

• If and when Oxford activates, delegates can start voting for (On) or against (Off) the feature activation of the changes listed above in each block they bake. They can also abstain with a Pass vote.
• These votes are cast by block-producing delegates, and are included in block headers.
• Participation is not mandatory, defaulting to Pass in the absence of signaling.
• The feature activation vote has two phases: a Voting phase and a subsequent Adoption phase.
• The Voting phase is driven by an Exponential moving average (EMA) whose half-life is 2 weeks. That is, it takes two weeks for the EMA to raise from 0% to 50% assuming only On votes are cast.
• The target threshold is a supermajority of 80% of On votes over On plus Off votes.
• There is no time limit or fixed duration for the Voting phase. It continues as long as the threshold is not met. There is no quorum either, the lack of participation (reified as Pass votes) is not taken into account by the EMA, and hence only affects the time required to reach the threshold.
• If the threshold is met, the Voting phase will complete at the end of the current cycle, and the Adoption phase will start at the beginning of the following cycle.
• The Adoption phase lasts 7 cycles. The beginning of the cycle following the end of the Adoption phase activates the guarded features.
• There is no automatic deactivation of the guarded features once in (and after) the Adoption phase — subsequent votes continue to be counted towards an updated EMA, but without any further effect.

NB In the implementation in the Oxford protocol, the issuance rate is computed 5 cycles in advance. Thus, in the first 5 cycles where is active, the protocol does not use the adaptive reward formula and keeps using the current reward values.