The focus of this blog post is on the automated extraction of an F* specification to OCaml and its execution as a QCheck Property-Based Test against an OCaml implementation. This work was done by Antonio Locascio during a 4 month internship at Nomadic Labs under the supervision of Germán Delbianco and Marco Stronati.
This work will also be presented at the ML 2022 workshop.
Introduction
A typical workflow when developing high-assurance software is to start with a prototype to better understand the problem at hand, write a specification for the desired system (having learnt from all the mistakes in the process of implementing said prototype), write a reference implementation of the specification, and then formally verify that the implementation matches the specification, a process that is slow and costly.
However in a fast paced development cycle, the not-yet-verified implementation is often sent to production, continues to be improved over time and becomes a moving target for the verification effort, which often does not bear fruit. This is not a new problem. One of the main goals behind the development of novel formal verification tools has been to reduce the cost of verification, to allow it to be better integrated in the development cycle (see for example proof oriented programming).
In many cases it is possible today to extract an implementation that matches a specification, thus merging the last two steps of the workflow described above.
Going a step further, we would like to start sketching a specification while we develop the prototype and use this model to test the prototype itself. Thus moving from a linear development process to an iterative one, where implementation and specification are constantly refined and adapted. While abstracting away implementation details in the specification, the verification gap problem arises: given that the verified model is loosely coupled with the implementation, do the properties that we have proved for the model really hold for the implementation?
One way of addressing the verification gap problem is to rely on Property-Based Testing (PBT), that is, to extract the model as properties that can be executed as tests on the implementation. The focus of this work is on a lightweight automated tool for extracting F* specifications to OCaml, and its execution as a QCheck test against an OCaml implementation. We propose to OCaml programmers to write specifications as F* programs, instead of manually writing QCheck tests. By doing this, our tool will automatically extract the specification as QCheck properties, which can then be used to test either the code extracted from the model, or another implementation.
Thanks to this approach, rather than waiting for a finished implementation and working on a complete formal verification, we can move along a verification spectrum. Start with a prototype implementation tested by PBT on its co-developed abstract model, refine the model over time in order to extract parts of it and replace them in the implementation until (possibly) a full extraction can be achieved.
It should be noted that a full extraction is sometimes too costly, as it may require the model to precisely represent complex parts of the code that are not essential to the program’s core functionality. However, being able to find the sweet spot along this spectrum where only the crucial parts have been verified is still very valuable and common practice.
Even where a full extraction can be achieved, the complex toolchains and large trusted computing base can still benefit from a testing infrastructure.
For example it is common practice to assume (and axiomatize) the existence of a List library that, during extraction, will be linked to the List module of the standard library, despite the fact that there is no formal connection between the two.
For this reason, even if our properties have already been proved in the model, they should also be tested in the extracted implementation.
In other words the verification gap may never be really closed in full, even at the end of the spectrum, and property based testing is a way to account for it in the development process.
The rest of the document is structured as follows: we first give a brief overview of the F* language and Property-Based Testing. Then, we give a detailed account of our proposed specification extraction tool for F*. After that, we present the case study for our workflow, Incremental Merkle Trees, which illustrates the wide spectrum of verification and testing strategies. Next, we describe our experience of working with F*, and explain our contributions to that project. Finally, we discuss related projects and some future work.
Overview
The workflow presented in this post, and the tooling developed, requires choosing a verification framework capable of extracting correct code to the target programming language, and a PBT library for the target language. In particular, given our OCaml codebase, we choose F* as a mechanization medium, and QCheck as a testing library. In the following, we give a brief overview of both systems.
An F* primer
F* is an ML-style functional programming language aimed at formal verification. F* combines automated verification through an SMT solver with the interactive functionality of a proof assistant based on dependent types, making it a hybrid verification tool. After the verification step, an F* program can be extracted to OCaml in order to be executed. Additionally F* supports meta-programming, which is mainly developed to support proving by tactics, but is a crucial feature for this work as it allows the extraction of specifications.
We’ll work through an example to introduce F*’s fundamental aspects. Let’s take a look at the following function, which reverses a list:
val reverse : list α -> Tot (list α)
let rec reverse l =
match l with
| [] -> []
| x :: xs -> reverse xs @ [x]
Those familiar with ML-style languages (such as OCaml) will straight away feel at home with F*’s syntax. One difference with OCaml’s syntax is that in F* signatures are usually given before a definition. These are a central aspect of F*, because of its rich type system.
One key feature of the type system is the effect system. Notice that in the return type of the example, Tot is an effect annotation, expressing that the function is total, pure and non-diverging. The generic shape of a function type in F* is α -> E β, where E is an effect. Additional built-in effects are: Dv, for diverging functions, ST for stateful computations, and ML for functions with arbitrary side-effects. Tot is the default effect, meaning that its declaration can be omitted.
Refinement types are another important part of F*’s type system. The refinement type x:T{φ(x)} is a sub-type of T for which all its inhabitants satisfy the property φ, also called the refinement. In other words, type x:T{φ(x)} is the type of values x from T for which φ(x) is true. For simplicity, we can assume that the predicates φ are total functions returning a boolean, although they can be more general. For instance, we can use them to give a more precise signature to our example:
val reverse : l:list α -> Tot (l':(list α){length l' = length l})
Here, we use the refinement type to state that we expect the resulting list to have the same length as the original one. To refer to the original list, we needed to name the argument (l) in the signature, making this a dependent function type.
F* provides an alternative syntax for writing a function’s pre- and post-conditions explicitly. Let’s look at it with a new example:
val tail : l:list α -> Pure (list α)
(requires (length l > 0))
(ensures (fun l' -> length l' = length l - 1))
Pure is just a version of the Tot effect that, in addition to the type of the return value (list α), is parameterized by a pre-condition (requires clause) and a post-condition (ensures clause). Then, this signature is equivalent to:
val tail : l:(list α){length l > 0} ->
Tot (l':(list α){length l' = length l - 1})
It’s not always desirable to pollute a function’s signature with properties about it. That’s when lemmas come into play. In F*, a lemma is a computationally irrelevant function (a total function returning unit), used to state some property about a program.
For example, we could state (and subsequently prove) that our reverse function is involutive with the following lemma:
val reverse_involutive : l:list α -> Lemma (l = reverse (reverse l))
A more detailed introduction to the F* language can be found in its tutorial.
Property-Based Testing with QCheck
Property-based testing (or PBT for short) is a testing discipline in which properties about programs are checked to be true by validating them on a large number of randomly generated examples. Property-based testing a program generally requires the user to do two things: (i) to define the desired properties about the code, and (ii) to provide functions for generating random inputs for those properties (commonly known as generators).
To aid the definition of these properties and custom data type generators, several libraries have been developed. One of these is QCheck, which offers a wide range of combinators to do PBT in OCaml. In this project we present a tool that automatically extracts QCheck properties from F* specifications. The generator definition, however, is still left to the user, as explained in the following section.
Specification Extraction Toolchain
Let’s start with some motivation for using a specification extraction tool. Say you have an OCaml program, or even an idea for one, and you want to write a specification for it. We propose that, instead of directly writing QCheck tests for it, you write the specification as an F* program. If you do this, our tool will automatically extract the specification as QCheck properties, which can be used to test both the code extracted from the model and the original implementation.
It’s not required to do a full verification of the code in order to use our tool. As previously mentioned, one could specify an abstract model of the implementation, whose properties could be tested against the more complex OCaml implementation. Further, one might even write the specification as an axiomatization of the implementation, i.e assuming the properties and leaving their actual proofs as a future step.
In order to extract a specification written in F* as properties for property-based testing we introduce a Meta-F* tactic called extract_spec, which is defined in the SpecExtraction module.
This tactic does two things. First, it extracts a function’s pre- and post-conditions as OCaml boolean functions. Second, it synthesizes the QCheck boilerplate code for defining the test.
Functionality
Before getting into the tool’s design, let’s take a look at a simple example of its usage. Its main functionality consists of extracting a function’s or lemma’s pre- and post-conditions as OCaml boolean functions. For instance, given the following F* function:
val foo : x:T{P1 x} -> Pure T' (requires (P2 x)) (ensures (fun y -> Q x y))
let foo x = ...
One can call the extract_spec tactic through a splice, which inserts syntax generated through Meta-F*. This is done by adding the following line (anywhere foo is in scope):
%splice[] (extract_spec (`%foo))
As a result, in the extracted OCaml code of the module where the splice was called, the following predicates will be defined:
let foo_pre = fun x -> P1 x && P2 x
let foo_post = fun x -> fun y -> Q x y
As shown in this example, a function’s pre-condition is parametrized by the function’s arguments, while its post-condition takes as an additional argument the function’s return value.
The second step, generating the QCheck tests, is performed by the make_test tactic (called by extract_spec). Continuing with the example, this tactic generates the following declarations:
let (gen_foo_args : T FStar_QCheck.arbitrary)
= FStar_QCheck.undefined_gen "Generator for foo's input not yet implemented"
let (test_foo_spec : FStar_QCheck.test_t) =
FStar_QCheck.test_make "foo_spec" gen_foo_args
(fun a0 ->
match a0 with
| x -> (FStar_QCheck.assume_ (foo_pre x);
foo_post x (foo x)))
The first of these corresponds to a template definition of the QCheck generator for foo‘s arguments. Deriving the generators is outside the scope of this project. Some discussion regarding this can be found in this issue.
The second is the definition of the QCheck test, in which the pre-condition is assumed and the post-condition is checked. The FStar_QCheck module is just a simple interface wrapper to expose some QCheck functions in F*.
Tool’s design
The tool’s design revolves around Meta-F* tactics. Meta-F* is a metaprogramming framework for F*, i.e. a library for manipulating F* terms from within F*. A tactic, then, is simply a function that uses Meta-F*.
The bulk of the specification extraction work is performed by the extract_spec tactic, which takes as argument the name of the function the user wants to extract a specification from. We’ll give an overlook of the algorithm it implements:
- The first step is to query the environment to get the function’s type. This could either be annotated in a signature or inferred by the typechecker.
- The retrieved type is subject to some (mostly trivial) transformations. The most interesting preprocessing step is synonym resolution (for example turning
natintov:int{v >= 0}), which is crucial to capture properties hidden in refinements. - Next, the type is traversed, one arrow at a time, collecting the names, types and refinements for each argument. For instance, for a type
x1:T1{P1 x1} -> x2:T2{P2 x1 x2} -> C,collect_argswill compute the list:[(x1;T1; fun x1 -> P1 x1); (x2;T2; fun x1 x2 -> P2 x1 x2)]. For each refinement we abstract all the previous binders. For now, we leave the final computationCuntouched. It’s important to note that an argument’s type might have nested refinements, e.g.x:(v:int{v >= 0}){x < 5}. In this step, these refinements are flattened to getfun x -> x >= 0 && x < 5. - All of the arguments’ refinements are then joined to get the function’s implicit pre-condition.
- Finally, the final computation type
Cis inspected. From it the post-condition (both from an ensures clause and the return type’s refinement) and potential explicit pre-condition (requires clause) are retrieved. When there is an explicit pre-condition, it is joined with the computed implicit pre-condition. There’s special treatment for lemmas, as in that case the post-condition doesn’t require an extra argument.
Most of this procedure is performed by the pre_post tactic defined in SpecExtraction.PrePost. The QCheck test boilerplate generation, defined in SpecExtraction.TestGeneration.make_test, is not discussed, as it’s mostly trivial syntax declaration.
Limitations
Our specification extraction tool has two limitations worth mentioning.
The first one is that only bool refinements are supported. This is necessary, as Type predicates might not be computable, for they can include universal and existential quantifiers anywhere in the term.
The second is that only pure functions work with the specification extraction mechanism for now. Although some other effect monads might be easily supported, this is not true in general. Supporting the ever-so-present ST effect, that carries a model of the heap in the type, for instance, doesn’t seem a trivial matter.
Case study: Incremental Merkle Trees
We applied our proposed workflow of verification and testing to the implementation of the Incremental Merkle Tree data structure, used in the Sapling protocol. This was a suitable target for our project, as:
- It’s a self-contained piece of code, whose only important dependencies are well-specified cryptographic primitives.
- The data structure has clear invariants, the preservation of which is not trivial.
- There are multiple implementations for it, of varying complexity, which help showcase the wide spectrum of verification and testing models.
We now proceed to give a brief introduction to Sapling and IMTs, before delving into a detailed account of our case study.
Sapling
Sapling is a protocol used in Tezos that enables privacy-preserving transactions of tokens. For storage purposes, this protocol uses the Incremental Merkle Tree data structure, or IMT. This IMT structure is simply a fixed height Merkle tree, in which the leaves are only stored on the last level in the leftmost positions and cannot be deleted. Because of their use in Zero-Knowledge proofs, the IMTs must always be considered to be full trees of fixed capacity. In the next section, we provide a more detailed description of IMTs. For more documentation, refer to the protocol’s specification.
In Tezos, there are currently two implementations of Sapling. The first one, found in lib_sapling, implements IMTs through purely functional ADTs. In contrast, the second implementation, which is part of the economic protocol, is written in a stateful style to make use of the protocol’s key-value storage. While the latter is more efficient, the former is simpler and thus easier to verify.
Incremental Merkle Trees
An Incremental Merkle Tree of height h contains 2^h leaves and h + 1 levels of nodes, with all leaves at level 0 and root at level h.
For now, we focus on the IMT implementation found in the Storage module from lib_sapling. This implementation includes the following definition of an algebraic data type tree to represent IMTs:
type tree = Empty | Leaf of C.Commitment.t | Node of (H.t * tree * tree)
This type of trees have commitments in their leaves and hashes (H.t) in their nodes. Although both of these have the same internal representation, they are differentiated because the commitments correspond to the values stored in the tree, while nodes’ hashes are used to preserve integrity (as in any Merkle tree).
The trees are always treated as being full, using the default value H.uncommitted 0 for unused leaves. All the nodes at the same level of an empty tree have the same hash, which can be computed from the default value of the leaves. These hashes are stored in the H.uncommitted list, so H.uncommitted n is the hash of an empty tree of height n.
To avoid storing huge empty trees, any subtree filled with default values is represented by the Empty constructor and given its height it’s possible to compute its hash using the H.uncommitted list. Because of this, we’ll sometimes refer to this representation of IMTs as compressed trees.
The leaves are indexed by their position pos, ranging from 0 to (2^h) - 1. The tree is incremental in the sense that leaves cannot be modified but only added and exclusively in successive positions from the leftmost to the rightmost leaf — i.e., from 0 to (2^h) - 1.
IMT F* Model
Commitments axiomatization
Let’s begin our dive into the model by focusing on the Commitments module. This interface axiomatizes the cryptographic primitives needed for IMTs, namely commitments and hashes. Here is where most of the model’s assumptions are introduced, most notably the following lemma:
val perfect_merkle : h:v_height ->
Lemma (ensures (forall h1 h2 h3 h4.
merkle_hash h h1 h2 = merkle_hash h h3 h4
==> h1 = h3 /\ h2 = h4))
which states that the assumed Merkle hash function is injective at every valid level (h). This property, which can be read as “if two outputs are equal, then their inputs must be equal”, models the absence of collisions in an ideal hash function.
This module interface’s OCaml realization (ml/Commitments.ml) is just a wrapper for the corresponding functions in lib_sapling.
Machine integers
The second aspect of the model we’ll discuss is the use of machine integers. Our initial version of the model was based on F* unbounded ints, which are implemented as Zarith ints. In order to make the model as close to the implementation as possible, we refined the specification using machine integer types, following the ones used in the OCaml code. This not only means that we prove the absence of arithmetic over/underflow in our model, but also that the extracted code should have the same performance (w.r.t. arithmetic operations) as the original implementation.
In the OCaml implementation from lib_sapling, both Stdint and OCaml native ints are used. For the former, F* already provides [U]IntN modules in the standard library, that are extracted to their Stdint counterpart.
Things are a little trickier for OCaml’s native int type, whose representation is architecture dependent. For this model, we assume a 64 bit architecture, so we need to deal with 63 bit integers. To do so, we provide an interface module Int63 following the structure of those provided by the standard library. We also include an OCaml realization for it (ml/Int63.ml), that implements them using the native int type.
Refining the specification using these representations of machine integers proved to be much smoother than what we initially feared. There was a downside, however, from an extraction point of view, which will be discussed in a future section.
Main Tree model
Now we can delve into the main part of the model for IMTs, defined in the Tree module. There are three important components that build up this model, each implemented as a sub-module. The first of these is Tree.Data, which introduces the underlying data type that we use to represent IMTs.
type tree α β : Type =
| Empty : tree α β
| Leaf : α -> tree α β
| Node : β -> l:tree α β -> r:tree α β -> tree α β
As implied by its name, the type tree models lib_sapling‘s type of the same name. The only difference is that in our model, the types of the values of the leaves and internal nodes are parameterized. For our IMT spec, α will generally be instantiated with the type for commitments and β with the one for hashes.
This tree type, then, is a direct translation of its OCaml counterpart. Things only start getting interesting when the type is refined with richer properties. Hence, in Tree.Properties the core properties used to specify IMTs are presented, alongside some lemmas about them. Let’s take a look at the two properties that give IMTs their name.
val incremental : h:C.v_height -> t:tree α β -> Tot bool
let incremental h t =
valid t && left_leaning t && balanced t && has_height h t
The first one is incrementality. This property essentially states that the leaves are filled in consecutive positions from left to right. Additionally, some other structural invariants are included in this property, such as the fact that no internal node should have two empty sub-trees. The next one, merkle, checks that the values in the internal nodes actually are the hashes of their sub-trees.
val merkle :
h:C.v_height ->
t:tree C.t_C C.t_H{valid t /\ has_height h t /\ balanced t} ->
Tot bool
(decreases %[v63 h])
let rec merkle h t =
match t with
| Empty -> true
| Leaf _ -> true
| Node ha l r ->
let hs = pred63 h in
ha = hash hs l r && merkle hs l && merkle hs r
With these two properties, we can define the following type:
type imt (h:C.v_height) : Type =
t:tree C.t_C C.t_H {incremental h t && merkle h t}
So, imt h is the type of incremental Merkle trees of height h. As we’ll see next, this type makes it quite simple and elegant to specify that a tree manipulating function preserves the IMT invariants directly on the function’s signature.
The third component of the core IMT model is Tree.Methods, where the functions that operate on IMTs are defined. We’ll focus on insertion, as it’s the only way to modify an IMT. The insert_list function, whose signature we show next, inserts a list of commitments into a tree. Its implementation is a model of insert, from lib_sapling.
val insert_list :
vs:list C.t_C ->
pos:uint32 ->
h:C.v_height ->
t:(imt h) ->
Pure (imt h)
(requires (length vs <= pow2 (v63 h) - UInt32.v pos
&& UInt32.v pos = count_leaves t))
(ensures (fun t' -> to_list t' = to_list t @ vs))
(decreases %[v63 h;0])
Let’s break down this signature. The first three arguments are quite simple: a list of commitments vs, the position pos of the tree in which those commitments will be inserted, and the height h of the tree (which is bounded by 32). Then, the function takes the initial tree t, which must be an IMT of height h. The return type first states that the function is Pure, meaning that it terminates and has no side-effects. After that, it describes that the function returns an IMT of height h. Finally, we have the requires and ensures clauses, which define additional pre- and post-conditions. For pre-conditions, the function requires that the list of commitments fits on the tree, and that pos is the next position to fill. As for post-conditions, we have that the list of elements of the resulting tree must be equal to appending vs to that of t. The decreases tag is just aiding the termination-checker.
It’s important to note that some pre- and post-conditions are implicit (those in the types of the arguments and return value), while others are explicit (requires/ensures clauses). In this example, the implicit properties are used to state the preservation of the IMT invariants, while the explicit clauses are reserved for the functional specification of insert_list.
Insertion identities
There were three insertion functions defined in the initial IMT specification:
insert_model: a naive implementation that checks if the left sub-tree is full to determine the path,insert_pow: an optimization carrying the next available position,insert_list: a further optimization for batch insertion. This is the one found in the OCaml implementation.
In the Tree.InsertionIdentities module the first two are defined, and all three are proven to be semantically equivalent.
Full Merkle Tree Translation
As explained in a previous section, our model uses a compressed representation of IMTs, following their implementation. An important verification target was to prove a translation from this representation to a standard Merkle tree model. To do so, we used the off-the-shelf Merkle tree model from F*, being able to adapt the Merkle properties proven in this model for our IMT type.
Certified OCaml implementation extraction
For the certified OCaml implementation, we need to extract the Tree.Data and Tree.Methods modules. The module ml/Tree.ml bundles these two extracted modules, and should replace the original OCaml implementation.
To perform the extraction, we just ask F* to extract these modules to OCaml. This will generate the OCaml files in _out/ containing the extracted code (alongside the extracted specification).
We can now take a brief look at some of the extracted OCaml code. First, the tree is extracted to the expected OCaml part.
type ('a, 'b) tree =
| Empty
| Leaf of 'a
| Node of 'b * ('a, 'b) tree * ('a, 'b) tree
More interestingly, the refined imt h type becomes:
type 'h imt = (Commitments.t_C, Commitments.t_H) Tree_Data.tree
Although the refinements are erased as expected, we’re left with a phantom type parameter h, which would be instantiated to unit in the rest of the extracted code. However, as the imt type is tagged with inline_for_extraction, it’s replaced by its definition. As for the insert_list function, the resulting OCaml code is:
let rec (insert_list :
Commitments.t_C list ->
Tree_Data.uint32 ->
Commitments.v_height ->
(Commitments.t_C, Commitments.t_H) Tree_Data.tree ->
(Commitments.t_C, Commitments.t_H) Tree_Data.tree)
=
fun vs ->
fun pos ->
fun h ->
fun t ->
match (t, (Int63.eq h (0)), vs) with
| (Tree_Data.Empty, true, v::[]) -> Tree_Data.Leaf v
| (uu___, uu___1, []) -> t
| (Tree_Data.Empty, uu___, uu___1) ->
insert_node (Tree_Data.pred63 h) Tree_Data.Empty
Tree_Data.Empty pos vs
| (Tree_Data.Node (uu___, l, r), uu___1, uu___2) ->
insert_node (Tree_Data.pred63 h) l r pos vs
Here we see that the final code looks quite similar to the original version, apart from some very clearly automatically generated names for the unused variables in patterns.
The extracted code has important shortcomings, some of which we managed to solve, as explained in a future section.
The Makefile target to run the extraction is:
make extract
Specification extraction and QCheck integration
In our concrete case, we put all the splices in a new module called Tree.PrePost.fst. This is not only helpful for organizing the extracted code, but also allows the user to verify the IMT model without running the specification extraction tactic (which can be slow).
In turn, running the splices will generate the OCaml file _out/Tree_PrePost.ml, containing the pre- and post-conditions and tests spliced with the extract_spec tactic.
We can take a look at the extracted property for insert_list‘s pre-condition:
let (insert_list_pre :
Commitments.t_C list ->
Stdint.Uint32.t ->
Int63.t ->
(Commitments.t_C, Commitments.t_H) Tree_Data.tree -> bool)
=
fun vs ->
fun pos ->
fun h ->
fun t ->
(((Int63.gte h (0)) &&
(Int63.lte h Commitments.max_height))
&&
((Tree_Properties.incremental h t) &&
(Tree_Properties.merkle h t)))
&&
(((Util.(Z.of_int << List.length) vs) <=
((Prims.pow2 (Tree_Data.v63 h)) - (Util.(Z.of_int << Stdint.Uint32.to_int) pos)))
&& ((Util.(Z.of_int << Stdint.Uint32.to_int) pos) = (Tree_Properties.count_leaves t)))
Although it may be somewhat hard to see at once, this is just the conjunction of the refinements in the function’s signature. Note that the << operator is just function composition.
Finally, we want to actually test the certified implementation against the extracted properties. To do so, we first complete the definition of the extracted QCheck generator templates, which can be found in the ml/generators.ml. Next, we copy the extracted QCheck tests in ml/test_internal_tree.ml. For instance, one of these tests is:
let (test_insert_model_spec : FStar_QCheck.test_t) =
FStar_QCheck.test_make "insert_model_spec" gen_insert_model_args
(fun a0 ->
match a0 with
| Prims.Mkdtuple2 (v, Prims.Mkdtuple2 (h, t)) ->
(FStar_QCheck.assume_ (insert_model_pre v h t);
insert_model_post v h t
(Tree_InsertionIdentities.insert_model v h t)))
These splices are executed by running:
make extract
To compile the tests, just run:
make test
This will generate an executable called test.exe in the _out directory, which runs the tests.
Testing the Protocol Sapling Implementation
As mentioned earlier, there are two Sapling implementations in Tezos. Up to now, we’ve solely focused on the one found in lib_sapling, for its relative simplicity. The other implementation is part of the Tezos Protocol, and is written in a stateful manner to make use of the Context (Tezos’ key-value store). This makes this IMT implementation much harder to verify directly than the ADT-based version.
This is a perfect opportunity to recall the verification spectrum we proposed in the introduction. The IMT implementation from lib_sapling sat at one end of this spectrum: it was easy to verify it directly and it could be replaced by the extracted OCaml code. The PBTs extracted from the specification in this case help close a somewhat narrow verification gap (mostly assumptions about machine integers, lists, cryptographic primitive and F*’s extraction mechanism).
The protocol version, on the other hand, stands at the opposite end of the spectrum. Due to its pervasive use of the Context and Lwt (an OCaml library for promises and concurrent I/O with a monadic interface), doing a full verification and replacing the code with the extracted specification becomes unfeasible. Then, the verification effort in this case is limited to a model of the implementation, whose extracted code then becomes a reference implementation against which the complex version can be tested. In our particular case, the work of specifying and verifying an abstract model for IMTs is already done, as we can use the work done for lib_sapling to this end.
Following this idea, we decided to test the protocol Sapling implementation against the certified and tested extracted ADT implementation. This is implemented on the ml/test/proto-test.ml module.
Several tests were considered, which are discussed in this issue.
The key to carrying this out was to define a projection function (project_tree) from the context tree representation to the IMT ADT. With this, we can describe the test we implemented with the following diagram:
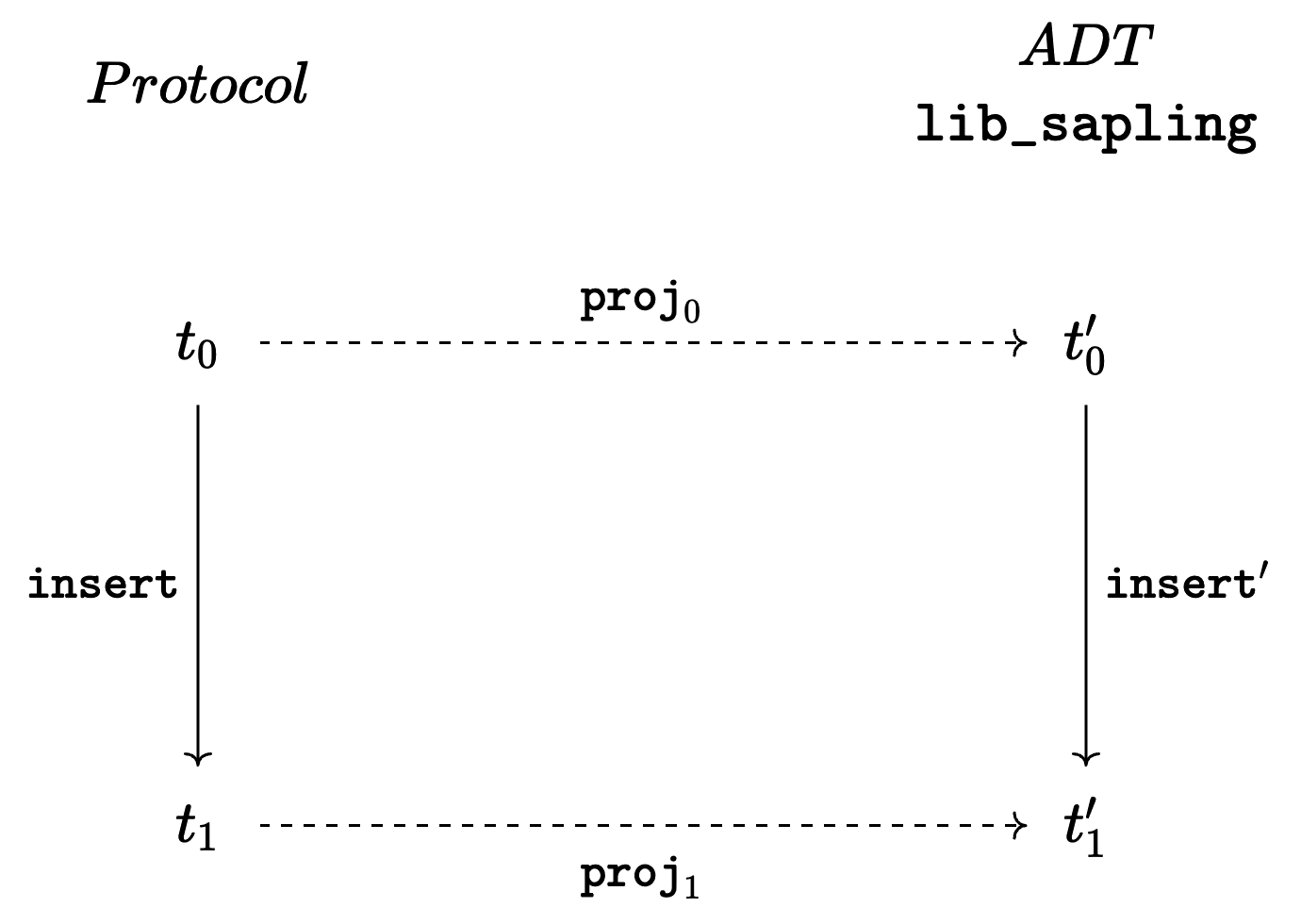
This diagram is divided in two by the vertical dotted line that delimits the protocol IMTs to the ADT IMTs. For instance, t0 stands for a context in which an IMT is stored, following the representation defined in sapling_storage.ml.
Here, proj0 and proj1 are calls to the projection function, and insert' is the IMT insertion function from our ADT spec (insert_list).
The function that we want to test is insert, the protocol IMT insertion (actually called add). Our test consists of checking the commutativity of this diagram. This means, to check that, for any given t0, proj1 (insert t0) is equal to insert' (proj0 t0).
By performing this test we ensure that the complex protocol insertion function is equivalent to the one we know is well-behaved, modulo the projections.
Our experience of working with F*
In this section we’ll summarize our experience with the F* language, and outline our contributions to the F* project.
General evaluation of F* for verifying OCaml code
One aspect that makes F* suitable for verifying OCaml code is the similarity of their syntax and type system. However, F* is not a superset of OCaml, so the modelling of a piece of OCaml code requires some varying degree of manual work. This will depend on the source program, as the translation of certain OCaml constructs (such as functors) is not trivial. In our experience, this process was quite straightforward, but that might not be the case for code bases that make heavy use of first-class modules.
Another of F*’s key selling points is its hybrid nature. The language’s SMT support did in fact allow for many of our model’s properties to be proven with little to no work, while being flexible enough to spell out more complex proofs. This, however, came at a cost. Overreliance on the SMT backend often led to increasingly flaky (i.e. unstable) proofs. A small change in a seemingly unrelated lemma might cause a previously proven theorem to no longer be accepted. This issue is often exacerbated by uninformative error messages that require some deciphering, which might negate some of the time savings gained by proof automation. All this should not be read as taking merit away from F*’s hybrid approach, but rather as a remark on the importance of finding the right balance between explicitness and reliance on automation when writing a proof.
Contributions to F*
As previously mentioned, during the duration of this project we encountered some of F*’s rough edges, which are to be expected in a research language. After discussing them with some of the language’s designers we agreed to try to provide solutions for some of these shortcomings, under their guidance. We can split these contributions into two groups.
Extraction of machine integers
After going to the trouble of refining the specification with machine integer types, it came as a surprise that the extracted OCaml code using machine integers was quite inefficient.
This was mainly due to how machine integer constants were extracted. The code generated for a literal such as 42l was the following:
FStar.Int32.int_to_t (Prims.of_int 42)
where int_to_t is defined as:
let int_to_t x = Stdint.Int32.of_string (Z.to_string x)
This means that for every machine integer constant, the extracted OCaml code would:
- Convert it to a Zarith int,
- Convert that Zarith int into a string, and
- Parse that string to get the desired Stdint int.
This added a significant unnecessary overhead, considering that the same can be achieved by the code:
Stdint.Int32.of_int 42
This was precisely the solution we implemented in PR FStar/#2325, which has already been merged.
A particular case of this issue was the extraction of 0 and 1 constants, which followed a similar logic. These cases are special, because all the Stdint modules, which implement F*’s machine integers, expose zero and one constants. So the solution for this was much easier: to add these constants to the machine integer interface. This is implemented by PR FStar/#2306, which is also merged.
Another source of inefficiency is the Int.Cast module, that defines the conversion between machine integer types. The issue here is almost the same as in the extraction of literals. For casting a value of a machine integer type to another, the extracted code converts the value into a string, parses the string into a Zarith int, which in turn gets converted into a new string that finally gets parsed as a value of the desired type. Again, this means that casting has a significant overhead. This can be avoided by providing OCaml realization for this module, instead of extracting it. The realization can use Stdint casts directly, improving its performance. We implemented this on PR FStar/#2315, which hasn’t been merged yet.
Meta-F*
The biggest contribution we made to F*, and the most crucial to our project, was adding support for mutually recursive let-bindings to the reflected syntax. Reflection allows inspecting, manipulating and creating F* terms from within F*, and was the tool we used for extracting specifications.
However, F*’s reflection AST didn’t support mutually recursive let-bindings, so our toolchain wouldn’t work for the function we cared the most about (insert_list).
After discussion with the F* team, and several iterations, we arrived to the solution in PR FStar/#2291, which has already been merged. This was a (though slight) breaking change, so we also had to fix some uses of the reflection interface in PR HACL-star/#471.
Finally, we encountered an issue when extracting polymorphic functions built through Meta-F*. In short, if a function’s type had more than one universally quantified type variable, then all except the first one would be instantiated as unit in the extracted code. We solved this issue in PR FStar/#2305, which is yet to be merged, but has already been reviewed. Although the fix is quite small, finding the source of this error took some time.
Unsolved issues with F*
Even though we managed to overcome the limitations of F* outlined in section [ref to section], there’s still one problem with the extracted OCaml code: its reliance on fstarlib (the OCaml implementation of F*’s standard library).
The issue lies in the fact that the extracted code uses fstarlib even when that could be avoided. For instance, primitive types (such as bool) are extracted as their F* standard library symbols (Prims.bool), instead of being extracted directly to their OCaml counterpart. Although both alternatives are semantically equivalent — Prims.bool is defined as a synonym to bool — this means that the extracted OCaml code will depend on fstarlib, even if the only part of the standard library that is used is the primitive types. Then, if one wanted to plug a module extracted form F* into an existing codebase, a number of possibly unnecessary dependencies needed by fstarlib might be added (e.g. batteries, yojson), greatly hindering the adoption of such a workflow.
There are possible, though unsatisfactory, workarounds to this issue. One of them is to manually tinker the extracted code to avoid the uses of the F* types, which is essentially what we did with the cleanup script. It goes without saying that doing this somewhat defeats the purpose of having a certified implementation, so one has to be very careful when doing so.
Discussion and Related Work
Before we go, we discuss projects that address similar problems through different approaches.
Extraction vs Lightweight Validation
Another well-established workflow is to directly extract correct implementations automatically from mechanized implementations. Projects like the Verified Software Toolchain narrow the verification gap by building a vertical stack of mechanized components, building on the foundations provided by the Compcert certified C compiler. Closer to F*, the KaRaMeL project allows the extraction of certified programs written in Low*, a subset of F*, to C.
Even when this approach has been successfully adopted in large industrial contexts, such as the verification of the seL4 micro-kernel, it would be hard to apply to a codebase like Tezos’, which is naturally designed to evolve. Instead, we propose to tackle the verification gap by leveraging the automated extraction of property-based tests from a formal specification in order to validate that the implementation complies with their formal model.
QuickChick
QuickChick is a randomized property-based testing plugin for the Coq Proof Assistant. Its central idea is foundational testing, which means that the testing code is formally verified to be testing the desired property. Additionally, QuickChick supports automatic derivation of generators for data satisfying a particular predicate. Our approach is more light-weight: implementing QuickChick’s features for F* would have required a very significant effort, and QCheck was already integrated into the Octez test suite.
There has also been some recent work leveraging QuickChick for testing OCaml code. Their workflow is the opposite of ours: they use coq-of-ocaml to translate OCaml definitions into Coq, and then rely on QuickChick to test the implementation. Moreover, this approach suffers from the limitation that coq-of-ocaml cannot fully translate all OCaml features into Gallina (Coq) without making arbitrary design decisions which carry
semantic weight.
Monolith
Monolith is a framework for testing OCaml libraries, that supports random testing and fuzzing. The user has to specify the library’s interface (types and operations) and provide a reference implementation. Then, Monolith runs sequences of operations trying to find unexpected behaviours.
Given that we propose extracting reference implementations from formally verified abstract models, it would be interesting to study if those could be integrated with Monolith. This way, the open issue of defining generators could be solved by making use of Monolith’s fuzzing and random testing features.
Extracting effectful specifications
Currently, our tool targets only pure F* programs with Boolean pre- and post-conditions. An interesting line of future work would be to extend it to support other F* monadic effects, and to leverage the specification extraction mechanism to test arbitrary monadic OCaml code implementing such effects. For example, in our setting this could be used for directly extracting a specification for the more complex stateful implementation of Incremental Merkle Trees.
