The case of mixed forks in Emmy⁺

Note: This analysis was done with the help of Bruno Blanchet (Inria). The interested reader can experiment with our code used in the analysis. As in the previous analysis, we do not present any security proofs.

This is the fourth in a series of posts on Emmy⁺:

1. After our initial analysis,
2. recently revisited and
3. extended to the partial synchronous network model,
4. we now consider so-called “mixed forks”.

So far, we assumed that malicious bakers wanted to undo a transaction. In this post, we consider instead that they want to maintain a (malicious) fork for as long as possible.

We provide experimental data that such scenarios do not have a significant impact on the previous analysis, which thus remains robust in the presence of this kind of attack.

Mixed forks

\(\newcommand\f[1]{\mathit{#1}}\) \(\newcommand\edelay{\f{delay}}\) \(\newcommand\edelaydelta{\edelay_{\Delta}}\) \(\newcommand\ie{\f{ie}}\) \(\newcommand\dpp{\f{dp}}\) \(\newcommand\de{\f{de}}\) \(\newcommand\dpde{\f{dpde}}\) \(\newcommand\od{\tau}\) \(\newcommand\emmy{\f{Emmy^+}}\) \(\newcommand\hb{H}\) \(\newcommand\cb{C}\) \(\newcommand\pr{\mathtt{Pr}}\) \(\newcommand\pprio[1]{\mathbb{P}_{prio}(#1)}\) \(\newcommand\pendo[1]{\mathbb{P}_{endo}(#1)}\) \(\newcommand\pdiff[1]{\mathbb{P}_{\Delta}(#1)}\) \(\newcommand\difff[1]{\f{diff}_{=1}(#1)}\) \(\newcommand\diff[1]{\f{diff}_{>1}(#1)}\) \(\newcommand\diffl[1]{\f{diff}_{\ell}(#1)}\) \(\newcommand\difffp[1]{\f{diff^{\leftarrow}}_{=1}(#1)}\) \(\newcommand\diffp[1]{\f{diff^{\leftarrow}}_{>1}(#1)}\) \(\newcommand\secu{\eta}\) \(\newcommand\barpc{\bar{\pc}}\) \(\newcommand\barph{\bar{p}^\star}\) \(\newcommand\tsh{t^\star}\) \(\newcommand\tsc{t}\) \(\newcommand\diffg{\f{diff}}\) \(\newcommand\pc{p}\) \(\newcommand\maxp{\f{max\_p}}\) \(\newcommand\ph{p^\star}\) \(\newcommand\diffgns{\f{diff}^{\;ns}}\) \(\newcommand\diffgs{\f{diff}^{\;s}}\) \(\newcommand\cchain{\f{ch}_\cb}\) \(\newcommand\hchain{\f{ch}_\hb}\)

For readability we introduce some notation: we use \(\hb\), resp. \(\cb\) to distinguish between honest and corrupt.

We can think of several dishonest bakers \(\cb_i\) as being a single ‘composite’ dishonest baker \(\cb\) having as stake fraction the sum of the stake fractions of \(\cb_i\), and similarly for the honest bakers.

So for simplicity, we reason henceforth using a pair of an honest baker \(\hb\) and a dishonest baker \(\cb\) acting as an adversary.

In our previous analyses (as above) we assumed \(\cb\) wants to undo a transaction, so:

1. \(\cb\) bakes a secret chain \(\cchain\) and
2. once \(\cchain\) is faster than \(\hb\)‘s chain \(\hchain\), \(\cb\) reveals it, and
3. honest \(\hb\) adopts \(\cchain\) and bakes on it thenceforth.

Now, suppose \(\cb\) wants to maintain the system in a forked state¹ as long as possible. So:

1. \(\cb\) still bakes a secret chain \(\cchain\),
2. \(\cb\) still reveals it once it is faster than \(\hchain\), and
3. \(\hb\) still adopts \(\cchain\) and bakes on it — but now,
4. \(\cb\) continues to secretly bake, this time on \(\hchain\).

The roles of the two chains are thus swapped, and that’s why we talk about mixed forks: the same chain may be \(\hb\)‘s chain at some point and \(\cb\)‘s chain at some other point, and this swapping of roles may happen more than once.

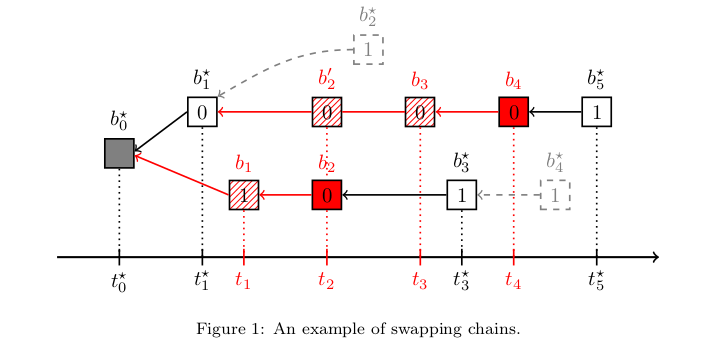
We illustrate such a scenario in Figure 1 below, where:

• Blocks (and their timestamps) baked by \(\hb\) are identified by the “\(^\star\)” superscript.
• Blocks baked by \(\cb\) are in red.
• The hashed red pattern denotes a block that \(\cb\) bakes but does not reveal.
• A block index represents the level at which the block is baked.
• The number in each block denotes the block’s priority.

We assume \(\cb\) has enough stake and chance to have consecutive 0 priorities for the blocks following \(b_1\), so that \(\cb\) can bake those blocks sooner than \(\hb\).

Figure 1 shows that:

1. At level 1, \(\cb\) starts a fork from \(b^\star_0\) by baking \(b_1\); \(\cb\) cannot reveal \(b_1\) because \(b_1\) has a larger timestamp than \(b^\star_1\) baked by \(\hb\).

2. At level 2, \(\cb\) double-bakes (bakes on its own secret chain and on the chain of \(\hb\)) and reveals \(b_2\), the block baked on its own secret chain before \(\hb\) bakes at this level (the block \(b^\star_2\) which \(\hb\) would have baked had it not been \(b_2\) is in gray, drawn with dashed lines).

3. At level 3, \(\cb\) bakes \(b_3\) on top of \(b'_2\) while \(\hb\) bakes \(b^\star_3\) on top of \(b_2\); \(\hb\) does so because \(\hb\) swapped chains once \(\cb\) revealed \(b_2\): at that point, \(\cb\)‘s alternative chain \(b_0^\star b_1b_2\) is longer than \(\hb\)‘s chain \(b_0^\star b_1^\star\).

4. At level 4, \(\cb\) bakes \(b_4\) on top of \(b_3\) and reveals it before \(\hb\) bakes at this level (note that we are in a similar situation as that at level 2).

5. At level 5, \(\hb\) bakes \(b^\star_5\) on top of \(b_4\): once \(\cb\) revealed \(b_4\), \(\hb\) swapped again chains because the alternative chain is longer than the one on which \(\hb\) was baking. This is the same reasoning as at level 3. Note that \(\hb\) bakes \(b^\star_5\) on the chain \(\hb\) initially started baking on.

\(\cb\) could in theory continue baking on both chains and force \(\hb\) to swap chains repeatedly, assuming \(\cb\) receives priorities and endorsement slots to allow it. We would thus like to quantify to what extent can \(\cb\) do that: how often and for how long.

Probabilities of mixed forks

To experimentally show that the probability that \(\cb\) can maintain a fork decreases (sufficiently rapidly) as fork length increases, we revisit the scenario “forks starting now”. We consider the following question:

How long can \(\cb\) maintain the system in a forked state?

To answer this, we use an approach similar to the one for computing the probabilities of forks in the non-mixed forks case. We presented the methodology behind the analysis in a previous post. However, the key aspects needing careful consideration are:

• how to identify when a swap is feasible and advantageous for \(\cb\), and
• how the update the time difference between chains at the moment of a swap.

Using our updated analysis, we plot the probabilities of mixed forks and compare them with the probabilities of non-mixed forks as already computed in the previous analysis). In this experiment we assumed that the network is synchronous.²

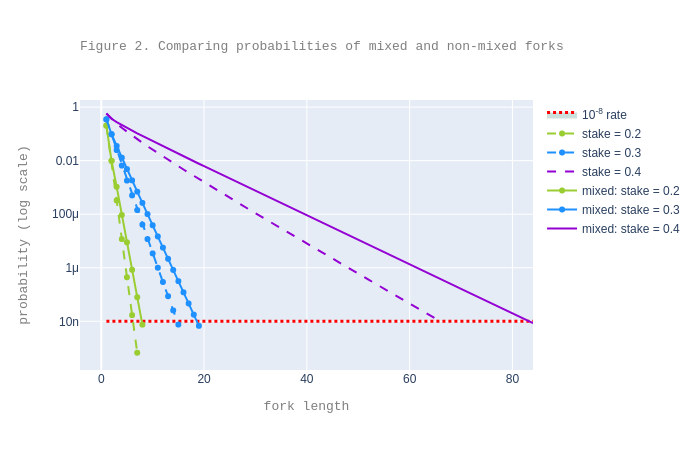
The plot suggests that, for decent attacker stake fractions such as .2, or even .3, the expected number of confirmations in the mixed case is only a bit larger than in the non-mixed case. For instance, for .3 attacker stake fraction, one needs to wait a priori for 20 confirmations instead of 16. The expected number of confirmations gets larger for higher attacker stakes: for .4, the expected number of confirmations is 85, vs. 67 for the non-mixed case.

To conclude, our experiments show that, even if \(\cb\) tries to repeatedly make \(\hb\) swap chains, \(\cb\) cannot do this for too long: the number of expected confirmations when considering “mixed forks” is only slightly higher than without them.